Escudo de la UCM

Departamento de Física Teórica I

U. Complutense de Madrid

Some research highlights of
Felipe J. Llanes Estrada

Escudo
de Físicas

Light Higgs, yet strong interactions 2014 Highlight of Journal of Physics G (published by the british IOP)	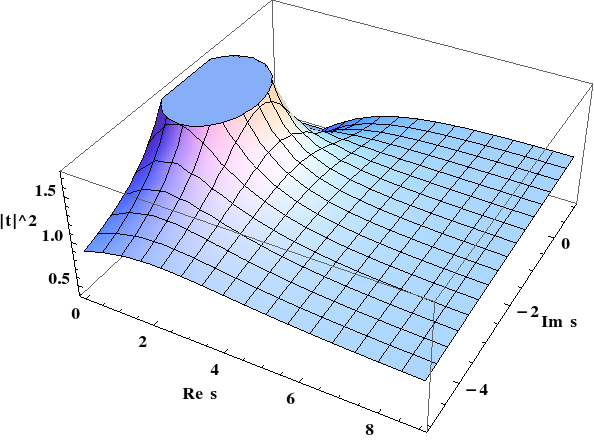	Heavy quark fluorescence: The Franck-Condon principle in heavy-hadron spectroscopy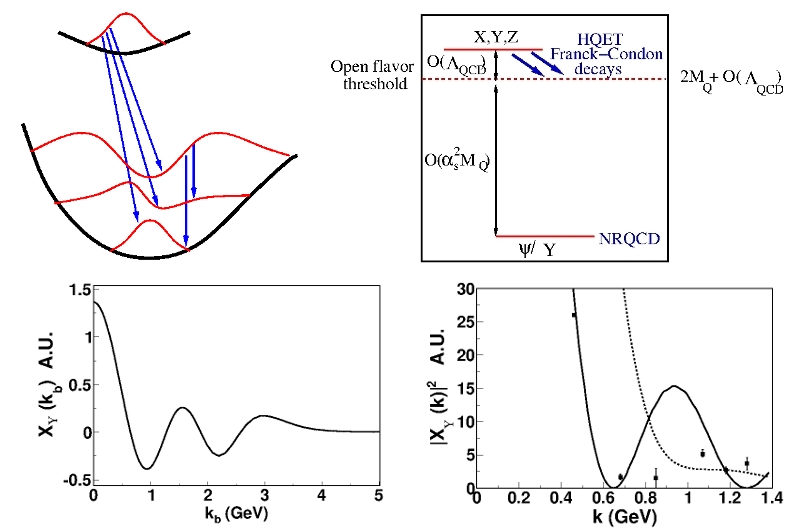
LHC experiments have found a mass gap in the particle spectrum above the 100 GeV scale, typical of the electroweak-gauge and newly found scalar-Higgs bosons. It may be the closure of the electroweak theory. But if further particles or interactions exist, because they are at E > 700 GeV, beyond the gap, they affect the known bosons indirectly by turning their mutual interactions stronger as energy grows from 100 GeV upwards. Our computed quantum mechanical scalar WLWL amplitude has modulus near 1 (the maximum allowed value it may take, a tell tale of strong interactions). We also find a second scalar pole in the scattering amplitude (shown) that would correspond to a second Higgs boson! But its width (inverse lifetime) is very large, making the particle interpretation of this pole very difficult. Technically: we have employed several unitarization methods to treat the generic tree-level amplitude low-energy effective Lagrangian with WL and Higgs, and a mass gap. We are now unitarizing the NLO chiral+Higgs chiral perturbative amplitudes.		A heavy meson contains a heavy quark-antiquark pair and in addition light quarks and gluons; when the meson decays strongly, the quark and antiquark separate, each landing on a product meson. The light degrees of freedom cannot alter the velocity of the heavy ones significantly, so the momentum distribution of the outgoing heavy-light mesons (bottom right, with what sparse Belle data there is) reflects the wavefunction of the initial meson (bottom left for a Cornell model Y(5S)). The available phase space for the BBpi decay of the Y(5S) allows for the first Sturm-Liouville node to be visible. The situation is analogous to the Franck-Condon principle of molecular physics (top left) where nuclei do not alter their momenta much in a radiative transition, because electrons are so light, so the electronic deexcitation leaves the molecule in a linear combination of the nuclear excitations over the electronic ground adiabatic potential where the nuclear momentum distribution is the same as in the parent molecule. The promise of the method is that it allows to disentangle conventional mesons from exotica in the very high spectrum, as it gives a window to the quarkonium internal structure.
Big open problem: there are seven new parameters in the most general (NLO) interaction among these particles even taking masses to zero, and no experimental guidance as to what their values are (nor even if they actually separate from the Standard Model). I am interested in whether/what new physics is beyond the SM, and particularly in reducing (not increasing!) its 25+ parameters.		Big open problem: we need to develop a systematic way to calculate corrections, the Franck-Condon principle is a Leading Order expression of some as yet undeveloped effective theory analogous to HQET. (Perhaps more data would fuel interest, there are not so many three or more body strong decays well measured for highly excited quarkonia.)

Heavy Ion collisions: correlations, transport, etc.		Why small groups in the Standard Model?

I have extensively analysed with Antonio Dobado and Juan Torres Rincon, then at Madrid, transport coefficients in the pion gas formed in the final stages of heavy ion collisions: the shear and bulk viscosity and thermal conductivity, that control how energy and momentum are transported relative to the almost conserved pion number where especially interesting (see the left plot with the conjectured universal minimum for the viscosity to entropy density ratio. Later we became interested in correlations and have been studying how they can be used to extract transport coefficients via the fluctuation-dissipation theorem, and bridging to cosmology (many properties of heavy ion collisions have analogs in the big bang theory). The right plot shows a public ALICE event: the color indicates average particle (transverse) momentum at that angular position in a Mollweide plot typical of cosmologists.		The gauge symmetry of the Standard Model is SU(3)_c x SU(2)_L x U(1)_Y for unknown reasons. One aspect that can be addressed is the low dimensionality of all its subgroups. Why not much larger groups like SU(7), or for that matter, SP(38) or E7? Our observation is that fermions charged under large groups acquire much bigger dynamical masses, all things being equal at a high e.g. GUT scale, than ordinary quarks. Should such multicharged fermions exist, they are too heavy to be observed today (that is what the figure shows: how the mass grows with the number of colors of the gauge group). They have either decayed early on (if they couple to the rest of the Standard Model) or become reliquial dark matter (if they don't). The result follows from strong antiscreening of the running coupling for those larger groups (with an appropriately small number of flavors) together with scaling properties of the Dyson-Schwinger equation for the fermion mass. You can download this work from here.
Big open problem: The traditional extraction via hydrodynamic simulations of heavy ion collisions suffers from systematic uncertainties due to the fluid modeling and unknown initial conditions. the extraction of transport coefficients from experimental correlations is not working very well yet, though our ALICE colleagues here in Madrid (CIEMAT), Victor Gonzalez, Pedro Ladron, and also Ana Marin at Heidelberg, are making an important effort.		We ran the computation from the Grand Unified scale down to the SM scales at one loop, which is probably insufficient precision to make a good estimate of what mass would fermions charged under dimension=4 groups (the next bigger ones beyond the Standard Model) have. It would be nice to have a more precise number: currently, O(1PeV).

Cubic neutrons in neutron stars?	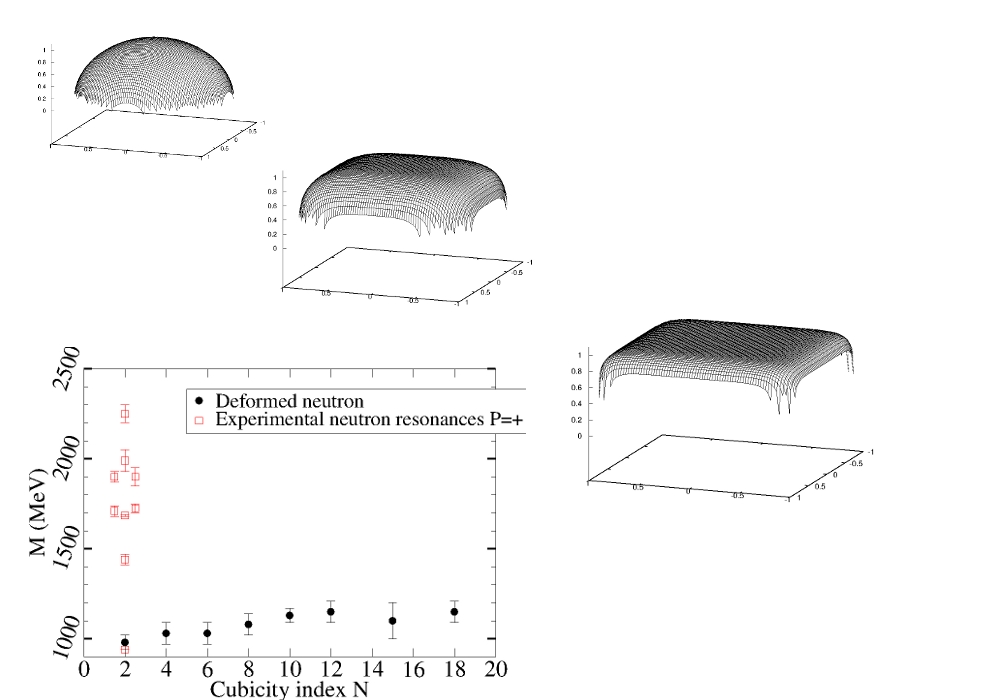	Symmetry breaking in quantum field theory:
Neutrons are finite-sized, largely spherical particles. But, as you have noticed in the market, oranges don't perfectly stack; Kepler figured out that at least a quarter of the volume is wasted. Under the extreme pressures of neutron stars, you gain energy = PdV if you deform neutrons keeping their volume constant, to fit them tighter. I calculated with Gaspar Moreno Navarro, a former Master student in U. Complutense de Madrid the cost of this deformation to be about 150 MeV. Technically, we substituted hyperellipsoidal trial variational wavefunctions for three-quark states in a standard global-color model of Coulomb-gauge QCD.		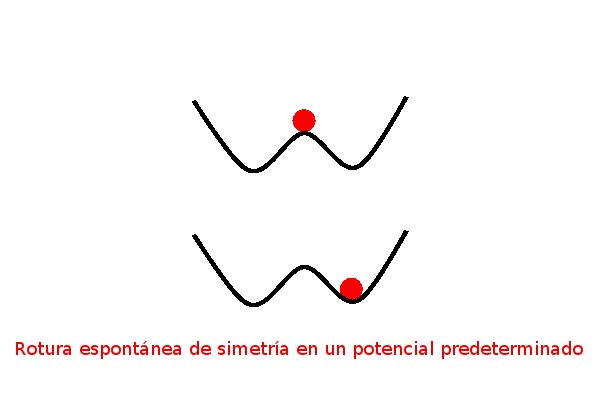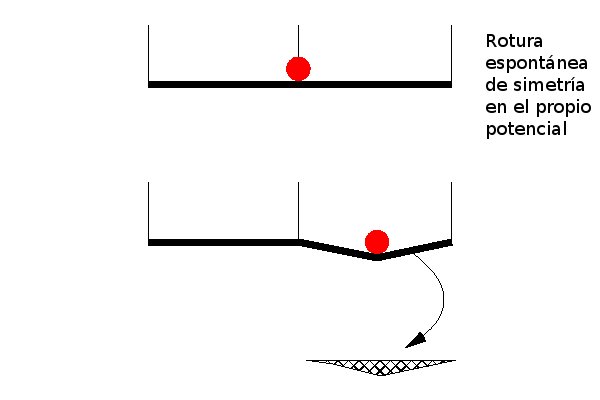The textbook explanation of Spontaneous Symmetry Breaking (top sketch): the potential is symmetric, but to minimize its energy, the bead must choose between left and right, so the physical state with least energy has less symmetry than the potential. My work with german collaborators (bottom sketch): the potential itself is determined dynamically, as exemplified by a bead on an elastic band that sinks under its weight. Technically, we approximated the Dyson-Schwinger equation for the quark-gluon vertex ("the potential") coupled to the DSE for the quark propagator ("the bead") and see how chiral symmetry breaks simultaneously in both.
Big open problem: the cost of the wavefunction deformation towards a cubic shape competes with other physical processes, for example the formation of a band gap (a color-conducting kind of solid state where quarks hop from node to node of a cubic lattice). I am investigating this question in atomic physics, where one hopes to "look up the answer" in a high-pressure laboratory. I am interested in many aspects of the structure of matter in neutron stars, and how to use them to constrain gravity. Saliently, Eva Lope Oter and I have developed a set of Equations of State specifically targeted at investigations beyond General Relativity: only hadron physics input has been used, no GR nor astrophysics. Visit the nEoS webpage.		Big open problem: the Dyson-Schwinger equations are an intertwined set of coupled equations with more and more particles (something like the GPKY hierarchy in statistical physics). Usually they are truncated at a low-level (in analogy to keeping only the Boltzmann equation). But since the coupling is strong, this is an unwarranted approximation in Chromodynamics. We only have a handle under a power-law infrared ansatz for all Green's functions, that allows inductive solution, but lattice gauge theory seems to yield finite infrared values disfavoring such ansatz. I am interested in many other aspects of the Dyson-Schwinger equations and generally of gauge theories.