monte carlo methods with constraints

The standard Monte Carlo simulation of systems displaying metastability is very inefficient, (think of first-order phase transitions , spin glasses, structural glasses, lattice polymers, etc.).

One may use constrained statistical ensembles in order to guide the simulation inside those rare but crucial regions were it does not want to get into. We combine a generalization of Lustig's microcanonical Monte Carlo with a fluctuation-dissipation formalism. Thermodynamic integration allows for an accurate reconstruction of the effective potential. Cluster algorithms can sometimes be made to work within this framework.

In the context of the Statistical Mechanics of disordered systems, this approach amounts to a redefinition of the quenched average in terms of an effective potential, rather than Gibb's free energy. This choice automatically cures the rare-events syndrome that has hampered progress for quite a long time.

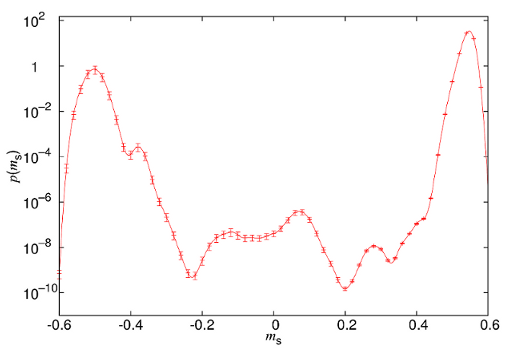
As an example, the figure shows the probability density function (pdf) of the so-called staggered magnetisation (the order parameter) of a diluted antiferromagnet in a magnetic field. Using our constrained Monte Carlo methods we are able to resolve the many peaks in this distribution, even though they have very different weights (notice the logarithmic scale).