Métodos simples
para el análisis de
puntos degenerados de
sistemas analíticos planos
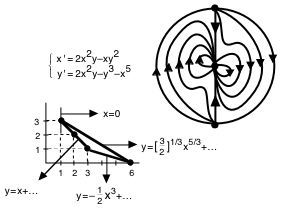
Métodos simples para el análisis de puntos degenerados de sistemas analíticos planos |
 |
|
|
(288 KB) |
|
(400 KB) | |
|
(392 KB) | |
|
(316 KB) | |
|
(192 KB) |
| 1. Introducción 2. Puntos críticos con un único autovalor cero 3. Análisis de puntos 'poco degenerados' 3.1. Utilizando la expresión en polares 3.2. Usando el blow–up: x=x , y=xv 3.3. Polinomios de tercer grado 3.4. La proximación homogénea para n=2 3.5. Polinomios de cuarto grado 3.6. La proximación homogénea para n=3 3.7. Ideas sobre estabilidad 4. ¿Centros o focos? 4.1. Sistemas homogéneos 4.2. Cálculo de la integral I para n=3 4.3. Centros y focos homogéneos para n=3 4.4. Inestabilización de centros elementales 4.5. Centros y focos no homogéneos y no elementales 5. Utilizando la poligonal 5.1. Ejemplos introductorios 5.2. Resultados generales 5.3. Aplicando los teoremas 5.4. Situaciones no recogidas en los teoremas 6. Análisis del infinito 6.1. Cambios de variable 6.2. El análisis homogéneo 6.3. Acudiendo a la poligonal 6.4. Ejemplos que exigen la poligonal 7. Referencias 8. Conclusiones |
5 9 15 18 21 27 29 34 42 51 55 59 64 79 85 100 107 110 117 130 136 147 150 154 158 162 177 181 |